#374. #6093. 「Codeforces Round #418」白金夜话
-
ID: 374
传统题
2000ms
256MiB
尝试: 0
已通过: 0
难度: (无)
上传者:
#6093. 「Codeforces Round #418」白金夜话
说明
给定坐标平面上 nnn 个圆。任意两个圆的边界至多只有一个公共点 —— 即它们必定相离或相切。
对于一个圆的集合，定义其异或面积为平面上被该集合中奇数个圆覆盖的图形面积。
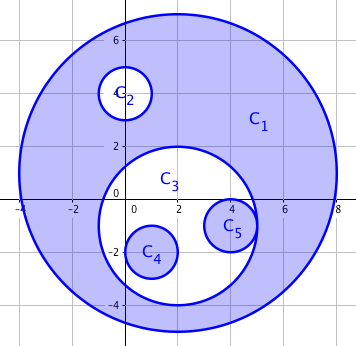
对于这个集合，浅蓝色部分图形的面积被计入异或面积内。
现在需要将这 nnn 个圆划分为两个集合，每个圆恰好在两个集合中的一个内。
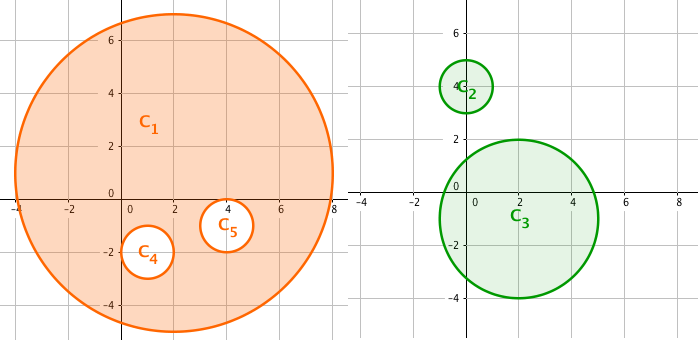
一种划分的方案，两个集合的异或面积如图所示。
请求出合法的划分方案中，两个集合分别计算的异或面积之和的最大值。
输入格式
输入的第一行包含一个正整数 nnn —— 圆的数目。
接下来 nnn 行，每行包含三个整数 xi,yi,rix_i, y_i, r_ixi,yi,ri —— 描述一个圆心位于 (xi,yi)(x_i, y_i)(xi,yi)、半径为 rir_iri 的圆。
输出格式
输出一个十进制实数 —— 合法的划分方案中，两个集合异或面积之和的最大值。
当选手答案与参考答案的相对误差或绝对误差不超过 10−910^{-9}10−9 时被视为正确。形式化地，若选手输出为 aaa，参考答案为 bbb，答案被视为正确当且仅当 ∣a−b∣max(1,∣b∣)≤10−9\frac{|a-b|}{\max{(1, |b|)}} \le 10^{-9}max(1,∣b∣)∣a−b∣≤10−9。
样例
样例输入 1
5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1样例输出 1
138.23007676样例解释 1
样例 1 的最优方案与「题目描述」一节中的图形对应。
样例输入 2
8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8样例输出 2
289.02652413数据范围与提示
1≤n≤10001 \leq n \leq 1\,0001≤n≤1000
−106≤xi,yi≤106-10^6 \leq x_i, y_i \leq 10^6−106≤xi,yi≤106，1≤ri≤1061 \leq r_i \leq 10^61≤ri≤106
* 熬夜有害身体健康